ライフプランニングをおこなうにあたり、将来得られる予想額を試算したり、将来用意したい金額に対して現在準備すべき額を試算するときに係数を使うことで簡単に計算をすることができます。
ライフプランニングをおこなう際に主に使用するのは次の6つの係数です。
係数を使うことで、今手元にあるお金や、将来目標としたい額に係数を掛けることで求めたい金額が簡単に計算できます。
係数については試験でほぼ毎年出題されるので、それぞれの係数の意味と計算の仕方はしっかり覚えておきましょう。
6つの係数
終価係数（しゅうかけいすう）
終価係数は、今手元にあるお金を複利運用した場合に、将来の元本と利息の合計額（元利合計といいます）がいくらになるかを算出するための係数です。
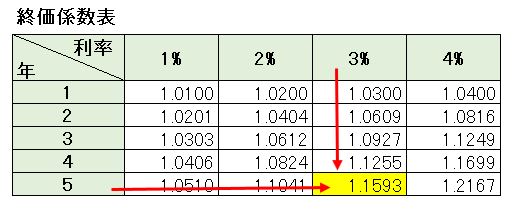
[box class=”box27″ title=”覚える！”]終価係数：現在の金額から将来の金額を求める[/box] [box class=”box8″]将来の金額 = 現在の金額 × 終価係数[/box]元本100万円を利率3%で複利運用した場合の5年後の元利合計を求めてみましょう。
終価係数表の中から5年と3%がぶつかるところ（黄色部分）の数値を100万円に掛けます。
すると、100万円を利率3%で5年間複利運用すれば 1,159,300円になると予想できます。
現価係数（げんかけいすう）
現価係数は、将来目標とする金額（元利合計）を達成するためにいまいくら元本が必要なのかを算出するための係数です。
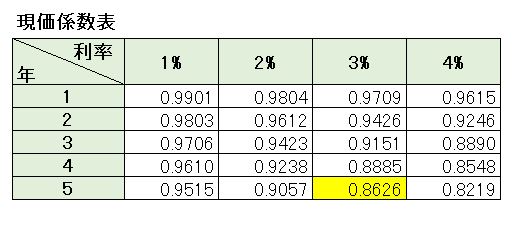
[box class=”box27″ title=”覚える！”]現価係数：将来の金額から現在の金額を求める[/box] [box class=”box8″]現在の金額 = 将来の目標金額 × 現価係数[/box]5年後に100万円に達したい場合、利率3%で複利運用した際にいま必要な元本はいくらあればよいのかを求めてみましょう。
現価係数表の中から 5年と3%がぶつかるところ（黄色部分）の数値を100万円に掛けます。
すると、5年後に100万円を手にするにはいま862,600円必要だということがわかります。
年金終価係数（ねんきんしゅうかけいすう）
年金終価係数は、毎年一定額を積み立てていった場合に将来積立合計額がいくらになるかを算出するための係数です。
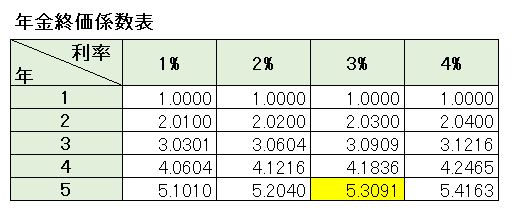
[box class=”box27″ title=”覚える！”]年金終価係数：毎年の積立額から将来の積立合計額を求める[/box] [box class=”box8″]将来の積立額 = 毎年の積立額 × 年金終価係数[/box]それでは、毎年100万円を利率3%で積立運用した場合の5年後の元利合計額を求めてみましょう。
年金終価係数表から 5年と3%がぶつかるところ（黄色部分）の数値を100万円に掛けます。
すると、毎年100万円を利率3%で積立運用した場合、5年後には5,309,100円になると予想できます。
減債基金係数（げんさいききんけいすう）
減債基金係数は、将来の目標金額を貯めるのに毎年いくら積み立てていけばよいかを算出するための係数です。
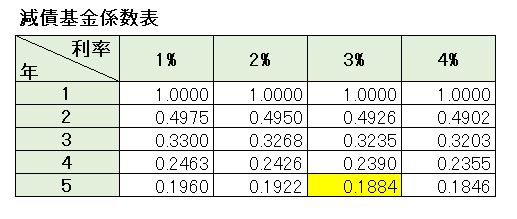
[box class=”box27″ title=”覚える！”]減債基金係数：将来の積立合計額から毎年の積立額を求める[/box] [box class=”box8″]毎年の積立額 = 将来の積立合計額 × 減債基金係数[/box]それでは、5年後に100万円に達したい場合に、利率3%で複利で積立運用した際に毎年いくら積み立てればよいのかを求めてみましょう。
減債基金係数表の中から 5年と3%がぶつかるところ（黄色部分）の数値を100万円に掛けます。
となり、5年後に100万円に達したい場合に、利率3%で複利で積立運用したとき、毎年188,400円積み立てればよいことがわかります。
資本回収係数 （しほんかいしゅうけいすう）
資本回収係数は、現在の年金原資を複利運用しながら受け取れる毎年の年金額や、借入額から利息を含む毎年の返済額を算出するための係数です。
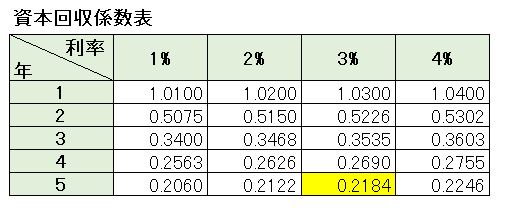
[box class=”box27″ title=”覚える！”]資本回収係数：現在の年金原資（または借入額）から毎年の受取年金額（または年間返済額）を求める[/box] [box class=”box8″]受取年金額（年間返済額） = 年金原資（借入額） × 資本回収係数[/box]それでは、1000万円を利率3%で複利運用しながら、5年間で均等に取り崩した（回収する）場合に毎年受け取れる額を求めてみましょう。
資本回収係数表の中から 5年と3%がぶつかるところ（黄色部分）の数値を1000万円に掛けます。
となり、1000万円を利率3%で複利運用しながら、5年間で均等に取り崩した場合 、毎年2,184,000円受け取れるということがわかります。
年金現価係数 （ねんきんげんかけいすう）
年金現価係数は、将来、希望する年金額を受け取るためにいま必要な資金の合計（年金原資）を算出するための係数です。
一定期間にわたって複利運用しながら希望の年金額を受け取るためには年金原資がいくら必要なのかを計算するために使用します。
また、年金現価係数は借り入れをする際に、年間の返済額から借入可能額を算出する際にも使用できます。
[box class=”box27″ title=”覚える！”]年金現価係数 ：毎年の受取年金額（または年間返済額）から必要な年金原資（または借入可能額）を求める[/box] [box class=”box8″]年金原資（借入可能額） = 受取年金額（年間返済額） × 年金現価係数[/box]それでは、利率3%で複利運用し、毎年100万円の年金を5年間受け取るにはいくら元本があればよいのかを求めてみましょう。
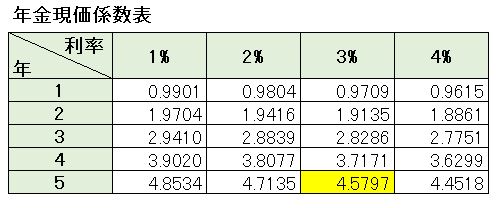
年金現価係数表の中から 5年と3%がぶつかるところ（黄色部分）の数値を100万円に掛けます。
となり、利率3%で複利運用し、毎年100万円の年金を5年間受け取るには4,579,700円の元本があればよいいうことがわかります。
係数のまとめ
以上の係数の意味をまとめると次のようになります。
| 名称 | 係数の意味 |
|---|---|
| 終価係数 | 現在の金額から将来の金額を求める |
| 現価係数 | 将来の金額から現在の金額を求める |
| 年金終価係数 | 毎年の積立額から将来の積立合計額を求める |
| 減債基金係数 | 将来の積立合計額から毎年の積立額を求める |
| 資本回収係数 | 現在の年金原資（または借入額）から毎年の受取年金額（または年間返済額）を求める |
| 年金現価係数 | 毎年の受取年金額（または年間返済額）から必要な年金原資（または借入可能額）を求める |
さらに、これらの係数は以下に示すように、将来の金額を求めるものと現在の金額を求めるものの2種類に分けられることがわかると思います。
それぞれ左右に並んでいる係数はお互い逆を求める関係になっています。
覚え方のコツとしては、「終」「収」と「しゅう」の文字がついているものは将来の金額を求める係数、「現」「減」と「げん」の文字がついているものは現在の金額を求める係数だと考えていただければよいでしょう。
